Homomorphic encryption
Contents
- Honoring Goldwasser and Micali
- Intro to encryption
- Homomorphic encryption
- A homomorphic encryption scheme
- Conclusion
Honoring Goldwasser and Micali
Shafi Goldwasser and Silvio Micali won the Turing Award recently, for their foundational work in cryptography. I had the pleasure of working with Silvio (as his TA and as his student) while at MIT, where he gave many of the most memorable and motivated lectures I’ve been part of.
In their honor, I’m writing a post which tries to teach some cryptography, to an even less technical audience. The topic I chose was Gentry’s construction of homomorphic encryption, for a few reasons:
- It was a huge breakthrough in cryptography
- It has a very nice proof idea
- I believe it can be well-illustrated to one with just high-school level math background (though I may not succeed at it)
- I’ve not seen a similar explanation attempted. (In particular, I’ve not heard Micali lecture about it)
Intro to encryption
Before we can talk about homomorphic encryption, we should talk about regular encryption.
History
Encryption in one form or another has been used for thousands of years. Notably, governments used ciphers to pass war messages.
In the 70s, it became much more commonplace, thanks to RSA, the famous encryption scheme which was developed by and named after another group of Turing award winners. (TAing for famous computer scientists is my main claim to fame, as I also did so for the R of RSA, Rivest.) Half a decade later, Micali and Goldwasser formally defined security for such schemes.
Today, we’ll need only a very basic presentation.
Encryption
Say we start with a message, call it \(m\). Like so:
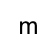
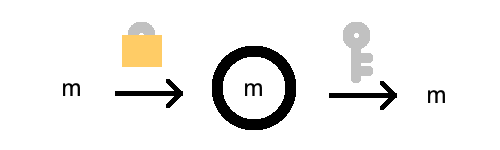
An encrypted message is just a message that is locked up so other’s cant read it. The message is not physically locked up, but is scrambled to look like complete gibberish. I’ll denote an encrypted message by drawing a circle around the original message:

Encrypting a message is the process of putting a lock around the message. The “lock” is actually a function you apply, called an encryption function.
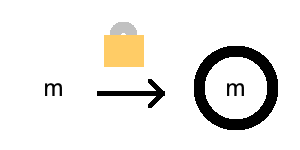
We’ll denote the encrpyted version of the message \(m\) by \(E(m)\). The function \(E\) is depicted by the lock. The arrow depicts function application.
Decryption
Now, a lock is not a lock without a key! With a certain secret key, this lock can be removed, and the message can be recovered!
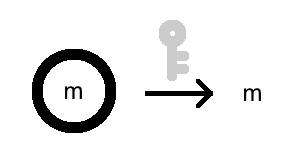
Decryption is also a function, call it \(D\). But in addition to a message, it also requires a secret key, \(k\).
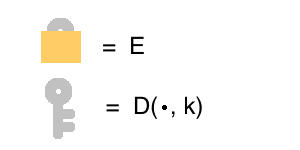
Crucially, decryption has the property that \(D(E(m), k) = m\). The picture makes it more obvious:
Equally important is that without this secret key \(k\), the message becomes very hard to recover. The function \(D\) is publicly known, but if you feed it the wrong key, you get gibberish back out.
As far as we can tell, you need to use brute force, which takes an impractically long time.

Note that encryption does not require the secret key. We call this “asymmetric” encryption. This asymmetry is very useful in the real world. For example, it lets me send a secret message to someone I don’t know, without knowing their key.
Summary
Encryption and decryption are fundamental to all security and privacy on the internet. In fact, RSA remains extremely practical and commonplace - if the security of the scheme were compromised, it would have a major impact on the world. Until then, it puts the S in HTTPS!
Homomorphic encryption
Homomorphic encryption is a different beast.
Motivation
Suppose Alice has a lot of private data, like her family’s sequenced genome, on a hard drive. But now she wants to search through it, or perform some more complicated algorithm on it. Unfortunately, her laptop isn’t powerful enough to run the whole computation. Bob offers an excellent cloud service for processing genomes. In fact, his proprietary algorithm is much better for extracting relevant information than the open-source algorithm Alice was thinking to run. But Alice doesn’t want to give away her genome to someone she doesn’t know. What does she do?
To solve this problem, we need something magical.
Definition
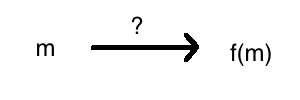
In general, suppose Alice wishes to apply some arbitrary function, \(f\), to some data, \(m\). Unfortunately, \(f\) can only be computed by Bob, perhaps because it is computationally expensive. However, Alice wishes for Bob not to see \(m\). So how can she get from \(m\) to \(f(m)\)?
Homomorphic encryption essentially lets you take encrypted inputs, and apply some function to get an encrypted output.
More precisely, homomorphic encryption is an encryption scheme, with an additional property. For any function \(f\), you can easily transform it into a “homomorphic” version of the function, call it \(f^*\). This transformation has the “homomorphic” property that \(f^*(E(m)) = E(f(m))\), for any message \(m\).
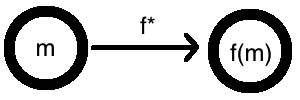
Of course, if you have a decryption key \(k\), this transformation from \(f\) to \(f^*\) is easy. Simply decrypt, apply \(f\), and re-encrypt! Formally, let \(f^*(x) = E(f(D(x, k)))\). Then, if \(x = E(m)\), we have \(f^*(E(m)) = E(f(D(E(m), k))) = E(f(m))\), as desired.
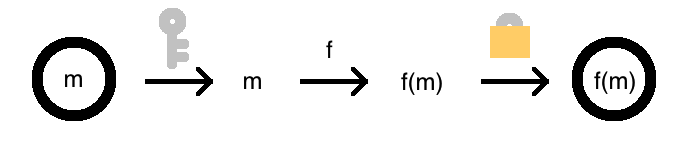
But in homomorphic encryption, the security of the original scheme is not compromised. So Bob is not allowed to use the key to accomplish this. After all, he is recovering \(m\) as an intermediate step, and could peek at it then.
In homomorphic encryption, he must compute a function on inputs he can’t even see, r esulting in an output he can’t see either! And this can be done for any function \(f\). The homomorphic property really is magical.
Now, assuming Bob has this way of transforming a function \(f\) into a homomorphic one \(f^*\), here’s how Alice would get \(f(m)\):

- Alice generates a secret, \(k\), and takes her data \(m\), and encrypt it, to get \(E(m)\).
- Alice hands \(E(m)\) to Bob, and tells him a function \(f\) she’d like to compute on it.
- As far as Bob can tell, \(E(m)\) is gibberish, since he doesn’t know \(k\). However, he transforms \(f\) into its homomorphic version, \(f^*\)
- Bob uses his super computer to apply \(f^*\) to \(E(m)\), producing \(f^*(E(m)) = E(f(m))\).
- Bob hands \(E(f(m))\) to Alice, who then decrypts with her key: \(D(E(f(m)), k) = f(m)\)!
In fact, if homomorphic encryption is possible, then Alice can even make the function itself secret. That is, she wants Bob to neither know \(f\) nor \(m\), and yet to compute \(f(m)\) for her! Can you see how? (Hint: it involves something called a Universal Turing Machine)
Homomorphic?
Now that you know what encryption is, and what homomorphic encryption is, you may be wondering what “homomorphic” means. In math, a homomorphism is a structure-preserving map. So “homomorphic” is a fancy way to say that it completes this diagram:
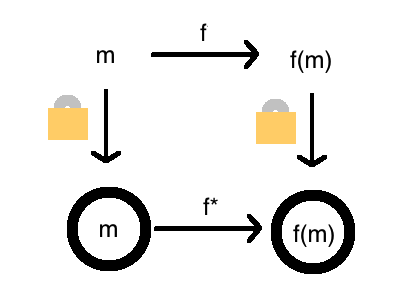
The homomorphic property lets us take the function \(f\) into a version of it that operates in an encrypted version of the world.
History
Homomorphic encryption is an incredibly useful tool, and is considered a holy grail of cryptography. While tons of encryption schemes were known by the 70s, nobody knew how to construct a homomorphic one. Often times, when things are too good to be true, theoreticians go ahead and prove it so. But nobody could show a homomorphic scheme was impossible either! So even with plenty of geniuses were thinking about it, homomorphic encryption was a huge question mark for 30 years.
… drumroll
A homomorphic encryption scheme
Finally in 2009, Craig Gentry produced a candidate homomorphic encryption scheme.
Somewhat homomorphic encryption
Coming up with a homomorphic encryption scheme is difficult, but it turns out coming up with a somewhat homomorphic scheme is not so hard.
In a somewhat homomorphic scheme, each time you apply the homomorphic version of a function, the quality of the encryption gets a bit worse.
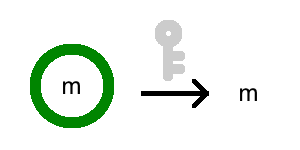
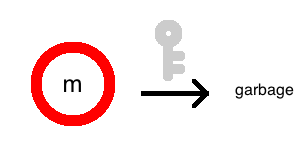
Imagine you could change the contents inside the lock, but the shape of the lock gets a little bit warped. The more complicated the function, the more warped the lock would get. For a while, the key might still be able to open the lock, but eventually, when the lock is too damaged, the key would stop working.
To illustrate, I’ll use green circles to denote locks that can still be unlocked, and red circles to denote locks that are hopeless. So a dark green circle is a perfectly fine encryption:
But a red one makes it so even a key can’t recover a message:
Now suppose we wanted to go from \(m\) to \(m + 6\), by repeatedly adding one. So, we let \(f(x) = x + 1\), use the homomorphic property to get \(f^*\), and apply repeatedly. What happens is this:

Recall that the homomorphic property is that \(f^*(E(m)) = E(f(m))\). Let \(E_x(m)\) represent an encryption with \(x\) amount of warpedness. So \(E_0(m)\) would represent a fresh encryption and \(E_6(m)\) might represent a irrecoverable encryption. The somewhat homomorphic property then says \(f^*(E_x(m)) = E_{x+y}(f(m))\), where the value of \(y\) depends on how complicated \(f\) is.
So I can homomorphically add 2 or 3, but not 6! This “somewhat homomorphic” property seems not so useful. But this was Gentry’s first step in obtaining a fully homomorphic scheme. So where do we go from here?
Bootstrapping
Suppose we had a way to “refresh” a bad encryption back into a good encryption.
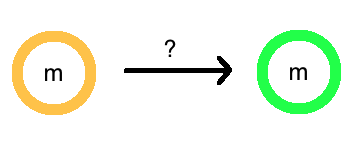
Then we could add 6 by simply adding 3, refreshing, then adding 3 again. More generally, we could decompose complicated functions into many simple functions, and refresh the encryptions after applying each simple function.
Here’s where an amazing idea called bootstrapping comes in. First, the picture:
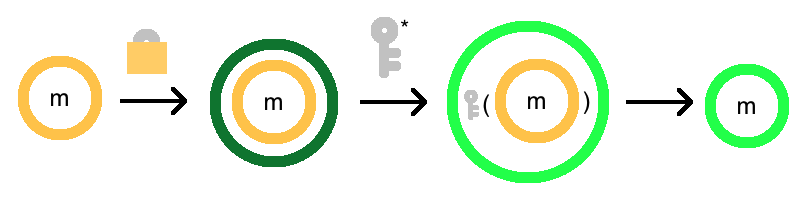
What the hell is going on here?
Basically, we’re putting a fresh lock on the outside, and then unlocking the inner lock. Unfortunately, when we do so, the outer lock will get a bit warped. But if it’s better than the original lock, then we’ve made progress!
But wait a minute, didn’t we cheat by using the key? Well, not quite. We used the homomorphic version of the encryption function, which looks like this:
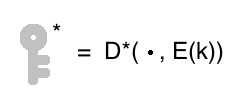
So Bob only needs an encrypted version of the key.

Is this safe? Cryptographers still believe this is okay, and that Bob can’t recover the key or message. It’s a bit like breaking into a house, where you know there’s a copy of the key inside the house. The fact that there’s a key inside doesn’t really help you, when you’re on the outside to begin with.
To break the bootstrapping process down in more detail:
- We start with an encryption that is getting close to unusable, \(E_4(m)\).
- We encrypt this encryption, freshly! So now, it is weirdly encrypted twice, as \(E_0(E_4(m))\). Bob can do this due to the asymmetric nature of encryption.
- We now homomorphically apply the decryption function! Remember, this means a function is magically applied to the inner contents. In this case, what’s inside is an encryption, and the function is decryption. So the result is that our original message sits inside just one lock! Mathematically: \(D^*(E_0(E_4(m)), k^*) = E_2(D(E_4(m), k)) = E_2(m)\)
The picture, again:

So this bootstrapping process turns a somewhat homomorphic encryption scheme into a “fully” homomorphic one, simply by doing this refreshing process repeatedly during our computation. And that’s it. Take a moment to understand - it’s really quite beautiful!
Aftermath
Plenty of technical work went into making the decryption function simple enough that the resulting lock wasn’t worse off than the beginning. But after Gentry’s original paper, the somewhat homomorphic schemes and decryption functions have actually been substantially simplified. The biggest key idea that opened the research floodgates was the bootstrapping.
So this amazing trick makes it so that we can now have someone blindly apply arbitrary functions to encrypted data. Unfortunately, this same trick makes the schemes impractically slow. The bootstrapping procedure is expensive and must be ran often, and nobody has figured out how to get rid of it. But research in this area has accelerating, and cryptographers are now working on bringing this dream to reality.
Conclusion
Imagine a world where
- cloud email services like Gmail could search through your mail for you without being able reading it, so you would never have to worry about the NSA pressuring Google into giving away sensitive information.
- voters could vote electronically without worrying about privacy (this is a special case of multi-party secure computation, which is possible with homomorphic encryption)
- you could give away truly obfuscated source code, but still let others run your algorithm
Can you imagine ways in which the world might be better off with homomorphic encryption?